Найти длину гипотенузы

Тема задачи: Стороны треугольника Создано: @alexcashtanov 4 октября 2015 07:46

Через середину гипотенузы прямоугольного треугольника проведен перпендикуляр. Отрезок этого перпендикуляра, заключенный внутри треугольника до пересечения с катетом, равен 3 см, а снаружи треугольника, до пересечения с продолжением другого катета 9 см. Найти длину гипотенузы

Оцените сложность задачи:
1 голосов, средняя сложность: 4.0000

Решения задачи

Создано: @nick 24 августа 2017 20:14
поставьте оценку:
1 голосов, средний бал: 5.0000

Через середину гипотенузы прямоугольного треугольника проведен перпендикуляр ...

ОтрезокMK3
ОтрезокKN9
Длина гипотенузыBC=2BM=2MC?
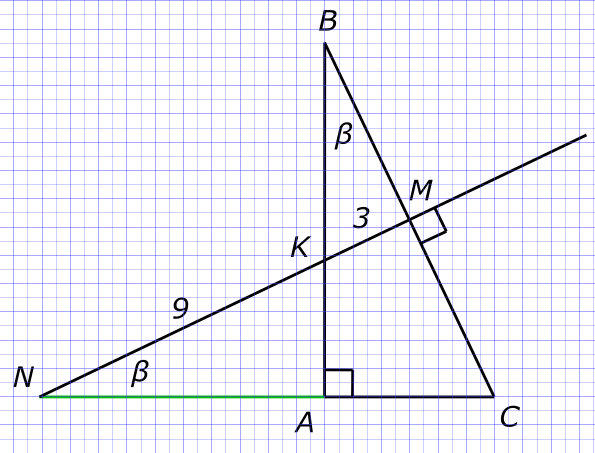
Изобразим на рисунке условия задачи

Изобразим на рисунке условия задачи

Прямоугольные треугольники ABC, KBM и MNC подобны так как

$ ⦟C ∈ ∆ABC и ∆NMC $

и углы образованные взаимно перпендикулярными сторонами

$ ⦟MNC = ⦟ABC = β $

как углы образованные взаимно перпендикулярными сторонами

$ ⦟BKM = ⦟BCA $

Из треугольника KBM

$ tg(β) = \frac{KM}{BM} $

Из треугольника NMC

$ tg(β) = \frac{MC}{MN} $

Приравниваем правые части уравнений

$ \frac{KM}{BM} = \frac{MC}{MN} $

Откуда находим

$ BM = \sqrt{(KM)(MN)}=\sqrt{(3)(3+9)}=6 $

И окончательно

$ BC = 2(BM) = 2 × 6 = 12 $

Ответ:

$ Длина гипотенузы равна 12 $

Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь

 Записать новую задачу Все задачи Все темы Все геометры