Найти площадь треугольника

Тема задачи: Нахождение площадей фигур Создано: @yagodka 6 октября 2015 09:17

Дан треугольник ABC. Известна его площадь S. Известен его периметр P. Прямые на которых расположены его стороны расходятся (треугольник увеличивается) на расстояние h. Найдите площадь увеличенного треугольника.

Оцените сложность задачи:
0 голосов, средняя сложность: 0.0000

Решения задачи

Создано: @nick 22 августа 2017 20:02
поставьте оценку:
0 голосов, средний бал: 0.0000

Данные задачи: треугольник ABC на расходящихся прямых

Площадь треугольника начальная
S
 
Периметр 
P
 
Стороны расходятся на расстояние 
h
 
Площадь треугольника увеличенная
S1
 		?
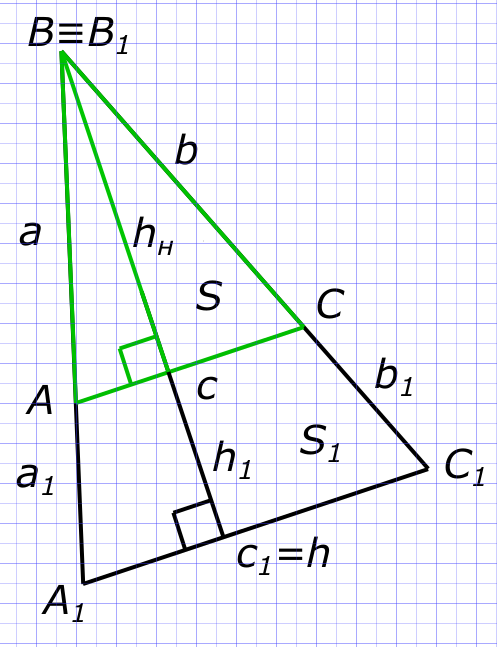
Изобразим на рисунке условия задачи

Изобразим на рисунке условия задачи

Треугольники ABC и A1B1C1 подобны так как

⦟A= A1; ⦟B= ⦟ B1; ⦟C= ⦟C1
 

и

AB
A1B1
=
BC
B1C1
=
CA
C1A1
= k
 

Площадь треугольника начальная

S=
1
2
chн
 

Площадь треугольника увеличенная

S1=
1
2
c1h1
 

Разделим первое уравнение на второе

S
S1
=
c
c1
×
hн
h1
= k × k= k
2
 

Откуда находим

S1=
S
k
2
 

Ответ:

Площадь треугольника увеличенная равна
S
k
2
 

Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь

 Записать новую задачу Все задачи Все темы Все геометры