Задачи на нахождение площадей фигур Активность в теме Нахождение площадей фигурСамые активные геометры в теме Нахождение площадей фигурЛучшие решения в теме Нахождение площадей фигурКак найти общую площадь пересекающихся круга и треугольника?
Для начала нарисую картинки. ситуация 1
$ a < R или a = R $ Треугольник полностью внутри круга или два его угла лежат на окружности.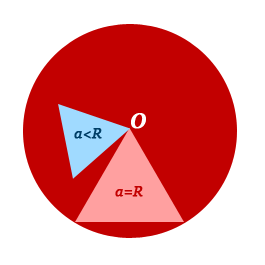 
рисунок 1 Общая площадь фигур равна площади круга.
$ S = \pi R^2 $ Найти площадь трапеции
Спустим перпендикуляр на AB из точки D.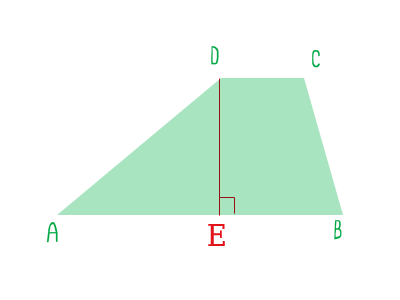 
рисунок 1 В треугольнике AED нам известно: формула 1
$ угол A = 30 градусов $ формула 2
$ угол E = 90 градусов $ формула 3
$ угол D = 180 - (30 + 90) = 60 градусов $ формула 4
$ гипотенуза AD = 16 $ Из прямоугольного треугольника найдем высоту DE формула 5
$ DE = AD * \sin(A) = 16 * \sin(30) = 16 * 0.5 = 8 $ Спустим еще один перпендикуляр на AB из точки С.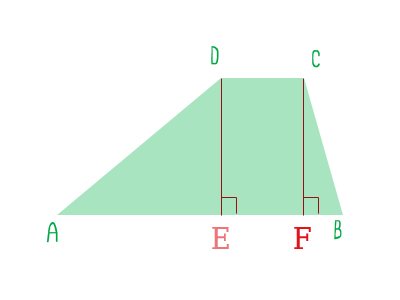 
рисунок 2 Вся фигура разбита на три фигуры: Треугольник AED, прямоугольник DEFC, и треугольник BCF. Сумма их площадей и равна искомой площади. Площадь треугольника AED формула 6
$ S_{AED} = \frac{1}{2} AE * DE $ Площадь прямоугольника DEFC формула 7
$ S_{DEFC} = DC * DE $ Площадь треугольника BCF формула 8
$ S_{BCF} = \frac{1}{2} BF * CF $ В треугольнике AED не хватает стороны AE формула 9
$ AE = AD * \sin(D) = 16 * \sin(60) = 16 * \frac{\sqrt{3}}{2} = 8 * \sqrt{3} $ формула 10
$ S_{AED} = \frac{1}{2} * 8 * \sqrt{3} * 8 = 32 * \sqrt{3} $ формула 11
$ S_{DEFC} = 4 * 8 = 32 $ В треугольнике BCF формула 12
$ FB = AB - (AE+EF) = 32 - (8 * \sqrt{3} + 4) $ формула 13
$ FB = 4*(8-2*\sqrt{3}-1) $ формула 14
$ S_{BCF} = \frac{1}{2} * 4 * (7-2 * \sqrt{3}) * 8 $ формула 15
$ S = 32 * \sqrt{3} + 32 + \frac{1}{2} * 32 * (7-2 * \sqrt{3}) $ формула 16
$ S = 32 * ( \sqrt{3} + 1 + \frac{7}{2} - \sqrt{3}) $ формула 17
$ S = 32 + 7*16 = 144 $ Ответ 144 КомментарииНайдите площадь параллелограмма.
площадь параллелограмма равна произведению основания на высоту. S=a*h, где a - основание параллелограмма, h - его высота. Из вершины тупого угла построим высоту к основанию, это васота h. Из полученного прямоугольного треугольника видим, что h равна 6 см. отсюда получаем, что площадь равна 14*6 и составляет 84 см2 площадь параллелограмма
$ S = a*h $ КомментарииНайти площадь сложной фигуры
Если соединить центры окружностей воображаемыми линиями, получается квадрат со стороной 2R, а его площадь: формула 1
$ S_{кв} = (2R)^2 = 4R^2 $ При этом от каждого угла квадрата отсекается четверть круга радиуса R. Отсеченных четветей круга всего четыре, итого отсечена площадь полного круга, т.е. формула 2
$ S_{кр} = \pi R^2 $ В итоге ответ такой: формула 3
$ S = S_{кв} - S_{кр} $ формула 4
$ S = 4R^2 - \pi R^2 = R^2 (4 - \pi) $ КомментарииНайти площадь равнобедренного треугольника
Данные задачи: равнобедренный треугольник
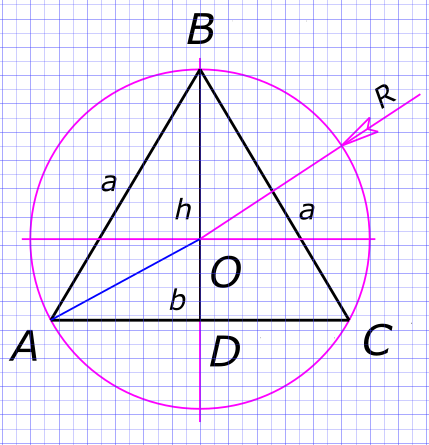
Изобразим на рисунке условия задачи Треугольник равнобедренный, поэтому центр описанной окружности
$ O ∈ BD $
$ OA = OB = R = 17 $
$ OD = BD - OA = 25 - 17 = 8 $ По теореме Пифагора
$ AD = \sqrt{(OA)^{2}-(OD)^{2}}=\sqrt{17^{2}-8^{2}}=15 $
$ b = AC = 2AD = 2 × 15 = 30 $ Тогда
$ S = \frac{1}{2}bh = \frac{1}{2}30×25 = 375 $ Ответ:
$ Площадь треугольника равна 375 $ КомментарииСложнейшие задачи в теме Нахождение площадей фигур Тема задачи: Нахождение площадей фигур
Найти площадь сложной фигуры
15 сентября 2015 12:45
0 подписчиков
1327 просмотров
1
решение Тема задачи: Нахождение площадей фигур
Найдите площадь параллелограмма.
13 ноября 2015 18:55
0 подписчиков
1378 просмотров
1
решение Тема задачи: Нахождение площадей фигур
Как найти общую площадь пересекающихся круга и треугольника?
10 сентября 2015 08:37
0 подписчиков
1058 просмотров
2
решения Тема задачи: Нахождение площадей фигур
Найти площадь трапеции
25 сентября 2015 10:41
0 подписчиков
1821 просмотр
1
решение Тема задачи: Нахождение площадей фигур
Найти площадь круга в который вписана трапеция
16 сентября 2015 12:32
0 подписчиков
804 просмотра
0
решений |
Записать новую задачу
Все задачи
Все темы
Все геометры
Темы с решениями
Нахождение площадей фигур
Решений 13
Задач 12
Нет подходящей темы
Решений 7
Задач 21
Геометрические задачи на максимум и минимум
Решений 3
Задач 3
Задачи по стереометрии
Решений 3
Задач 7
Прямоугольные треугольники
Решений 2
Задач 2
Нахождение объемов фигур
Решений 2
Задач 2
Нахождение периметра
Решений 2
Задач 2
|
Комментарии