Нет подходящей темы Активность в теме Нет подходящей темыСамые активные геометры в теме Нет подходящей темыЛучшие решения в теме Нет подходящей темынайти sin tan ctan.
Пример текста формула 1
$ \sin^{2}(\alpha)+\cos^{2}(\alpha) = 1 $ формула 2
$ \sin(\alpha) = \sqrt{1 - \cos^{2}(\alpha)} $ формула 3
$ \sin(\alpha) = \sqrt{1 - \frac{3}{4}} = \sqrt{\frac{1}{4}} = \frac{1}{2} $ формула 4
$ \tg(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} $ формула 5
$ \tg(\alpha) = \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}} $ формула 6
$ \ctg(\alpha) = \frac{\cos(\alpha)}{\sin(\alpha)} $ формула 7
$ \ctg(\alpha) = \frac{\sqrt{3}/2}{1/2} = \sqrt{3} $ Найдите синус, косинус и тангенс углов А и В треуголника АВС с прямым углом С
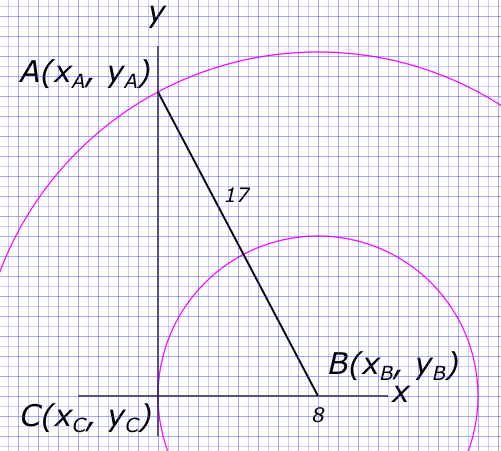
Изобразим на рисунке условия задачи a) Составляем уравнение длины гипотенузы прямоугольного треугольника
$ |AB| = \sqrt{(AC)^{2}+(BC)^{2}} $ Откуда находим
$ |AC|=\sqrt{(AB)^{2}-(BC)^{2}}=\sqrt{17^{2}-8^{2}}=15 $ Тогда:
$ sin(A) = \frac{AC}{AB}=\frac{15}{17}; $
$ cos(A) = \frac{BC}{AB}=\frac{8}{17} $ и
$ tg(A) = \frac{sin(A)}{cos(A)}=\frac{\frac{15}{17}}{\frac{8}{17}}=\frac{15}{8} $ КомментарииНайти длину радиуса умноженного на 3.
r = D / 2 * 3
r = 15 КомментарииНаписать уравнение медианы mА, проведенной из вершины А.
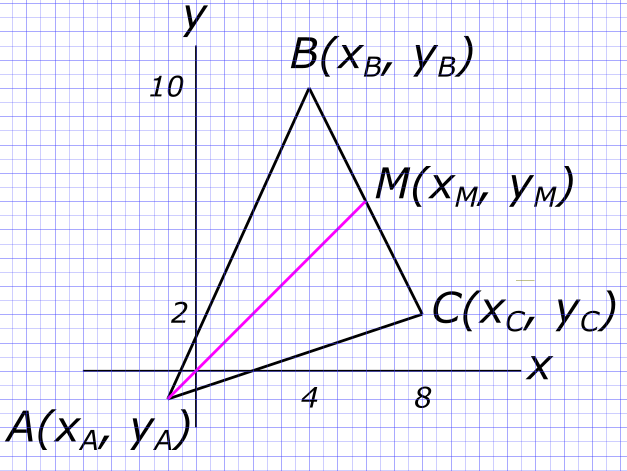
Изобразим на рисунке условия задачи Находим координаты точки M
$ M_{x} = \frac{x_{B}+x_{C}}{2}=\frac{4+8}{2}=6 $ и
$ M_{y} = \frac{y_{B}+y_{C}}{2}=\frac{10+2}{2}=6 $ Координаты точки M
$ M(6, 6) $ Уравнение прямой по двум точкам
$ \frac{x-x_{A}}{x_{M}-x_{A}} = \frac{y-y_{A}}{y_{M}-y_{A}} $ Подставляем значения
$ \frac{x-(-1)}{6-(-1)} = \frac{y-(-1)}{6-(-1)} $ или
$ \frac{x+1}{6+1} = \frac{y+1}{6+1} $ Откуда находим
$ y={6+1}\frac{x+1}{6+1}-1=x $ Ответ:
$ уравнение медианы: y = x $ КомментарииСложнейшие задачи в теме Нет подходящей темы Тема задачи: Нет подходящей темы
найти sin tan ctan.
4 декабря 2015 14:45
0 подписчиков
1261 просмотр
1
решение Тема задачи: Нет подходящей темы
Найти длину радиуса умноженного на 3.
31 октября 2015 20:47
1 подписчик
1087 просмотров
2
решения Тема задачи: Нет подходящей темы
Найти площу сегмента
16 ноября 2016 17:46
0 подписчиков
1039 просмотров
0
решений Тема задачи: Нет подходящей темы
Найти площу сегмента
16 ноября 2016 17:58
0 подписчиков
1023 просмотра
0
решений Тема задачи: Нет подходящей темы
Определить натуральную величину величину треугольника АВС. Методом замены плоскостей
9 января 2021 15:52
1 подписчик
1034 просмотра
0
решений |
Записать новую задачу
Все задачи
Все темы
Все геометры
Темы с решениями
Нахождение площадей фигур
Решений 17
Задач 12
Нет подходящей темы
Решений 7
Задач 24
Построение и исследование геометрических фигур
Решений 3
Задач 3
Геометрические задачи на максимум и минимум
Решений 3
Задач 3
Задачи по стереометрии
Решений 3
Задач 7
Прямоугольные треугольники
Решений 2
Задач 2
Нахождение объемов фигур
Решений 2
Задач 2
|
Комментарии