Задачи по стереометрии

Задачи по стереометрии Задачи
7 Задач в теме
3 Решений в теме
0 Подписчиков
О теме Новые Задачи Интересные Задачи Без Решения Интересующиеся

Задачи по стереометрии

Активность в теме Задачи по стереометрии

Самые активные геометры в теме Задачи по стереометрии

@NICK

@NICK

Задач 1
Решений 2

@fightfirewithfire7

Задач 1
Решений 1

Лучшие решения в теме Задачи по стереометрии

Найти расстояние от точки А до плоскости α
Создано: @fightfirewithfire7 24 апреля 2016 21:10
поставьте оценку:
2 голосов, средний бал: 5.0000

Треугольник АВН / h^2=АВ^2-BH^2=(x+1)^2-25 ACH / h^2=x^2-4 (x+1)^2-25=x^2-4; 2x+1-25=-9 2x=20;x=20/2; x=10 h= из под корня 400/4-4=из под корня 384/4= из под корня 96

Найти расстояние от точки А до плоскости α
Создано: @nick 10 августа 2017 20:10
поставьте оценку:
1 голосов, средний бал: 5.0000

Пример текста

Данные задачи: Из точки А к плоскости α проведены две наклонные

Наклонная ABx+1см
НаклоннаяACx
Проекция наклонной ABBD5см
Проекция наклонной ACCD2см
Расстояние от точки А до плоскости αh=AD?
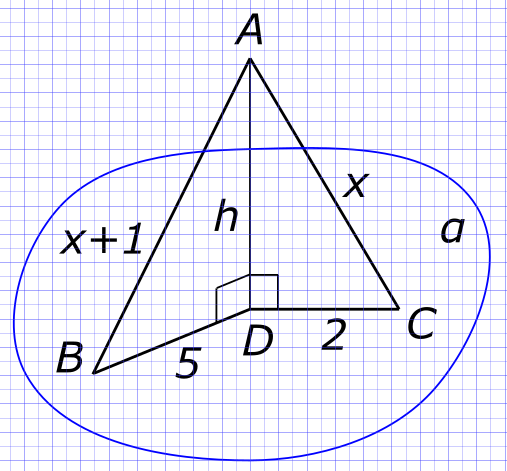
Изобразим на рисунке условия задачи

Изобразим на рисунке условия задачи

Из прямоугольного треугольника ACD

$ (AD)^{2} = (AC)^{2}-(CD)^{2}=x^{2}-2^{2} $

Из прямоугольного треугольника ABD

$ (AD)^{2} = (AВ)^{2}-(BD)^{2}=(x+1)^{2}-5^{2} $

Тогда

$ x^{2}-2^{2} = (x+1)^{2}-5^{2} $

или

$ x^{2}-4 = x^{2}+2x+1-25 $

Откуда находим

$ x = \frac{20}{2}=10 $

Тогда

$ AC = x = 10 см $

и

$ AB = x+1 = 10+1 = 11 см $

Находим расстояние, например из треугольника ABD

$ h = AD = \sqrt{(AB)^{2}-(BD)^{2}}=\sqrt{11^{2}-5^{2}}=\sqrt{96} см $

Ответ:

$ Расстояние от точки А до плоскости α равно \sqrt{96} см $
Определить боковую поверхность цилиндра
Создано: @nick 6 августа 2017 21:36
поставьте оценку:
0 голосов, средний бал: 0.0000

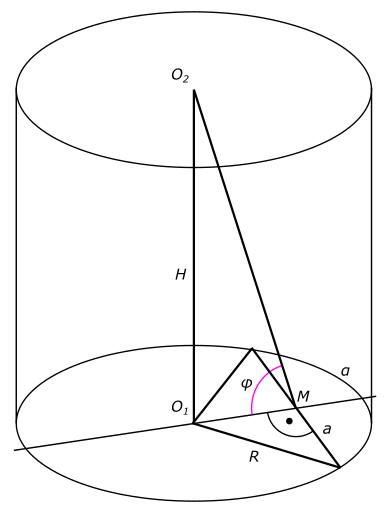
Изобразим на рисунке условия задачи

Изобразим на рисунке условия задачи

Составим уравнение боковой поверхности цилиндра

$ S_{б} = 2πRH $

Рассматривая половину треугольника в основании цилиндра, находим

$ sin(\frac{α}{2}) = \frac{\frac{a}{2}}{R} $

Откуда находим радиус цилиндра

$ R = \frac{\frac{a}{2}}{sin(\frac{α}{2})} $

и

$ |O_{1}M| = Rcos(\frac{α}{2})=\frac{acos(\frac{α}{2})}{2sin(\frac{α}{2})}=\frac{a}{2tg(\frac{α}{2})} $

Рассматривая треугольник O1O2M

$ tg(φ) = \frac{H}{O_{1}M} $

Откуда находим высоту цилиндра

$ H = (O_{1}M)tg(φ)=\frac{atg(φ)}{2tg(\frac{α}{2})} $

Подставляем найденные значения радиуса и высоты

$ S_{б} = 2π\frac{\frac{a}{2}}{sin(\frac{α}{2})}\frac{atg(φ)}{2tg(\frac{α}{2})}=\frac{πa^{2}tg(φ)}{2sin(\frac{α}{2})tg(\frac{α}{2})} $

Сложнейшие задачи в теме Задачи по стереометрии

Тема задачи: Задачи по стереометрии Найти расстояние от точки А до плоскости α
30 марта 2016 22:44
0 подписчиков
3088 просмотров
2
решения
Тема задачи: Задачи по стереометрии Определить боковую поверхность цилиндра
25 декабря 2016 11:26
0 подписчиков
3731 просмотр
1
решение
Тема задачи: Задачи по стереометрии Вы мне поможете???
3 мая 2016 19:27
0 подписчиков
1227 просмотров
0
решений
Тема задачи: Задачи по стереометрии Может ли плоскости α принадлежать...
21 октября 2015 12:19
0 подписчиков
1814 просмотра
0
решений
Тема задачи: Задачи по стереометрии Принадлежит ли плоскости третья вершина треугольнка?
21 октября 2015 12:16
0 подписчиков
2114 просмотра
0
решений
 Записать новую задачу Все задачи Все темы Все геометры

Темы с решениями

Нахождение площадей фигур Нахождение площадей фигур Решений 17 Задач 12 Нет подходящей темы Нет подходящей темы Решений 8 Задач 26 Построение и исследование геометрических фигур Построение и исследование геометрических фигур Решений 3 Задач 3 Геометрические задачи на максимум и минимум Геометрические задачи на максимум и минимум Решений 3 Задач 3 Задачи по стереометрии Задачи по стереометрии Решений 3 Задач 7 Прямоугольные треугольники Прямоугольные треугольники Решений 2 Задач 2 Нахождение объемов фигур Нахождение объемов фигур Решений 2 Задач 2