Определить боковую поверхность цилиндра

Тема задачи: Задачи по стереометрии Создано: @dmalivanova 25 декабря 2016 11:26

В нижнем основании цилиндра проведена хорда, длина которой равна а. Эта хорда стягивает дугу альфа. Отрезок, который соединяет центр верхнего основания с серединой проведённой хорды, образует с плоскостью основания угол фи. Определите боковую поверхность цилиндра

Решения задачи

Создано: @nick 6 августа 2017 21:36

поставьте оценку:

0 голосов, средний бал: 0.0000

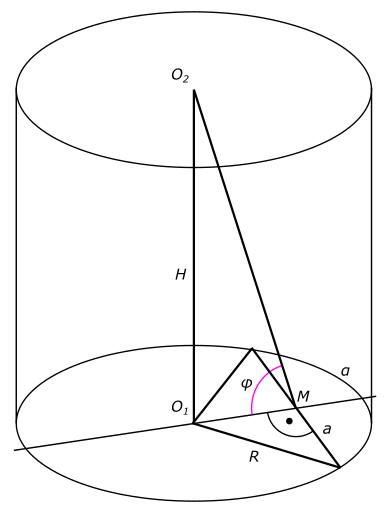
Изобразим на рисунке условия задачи

Составим уравнение боковой поверхности цилиндра

$ S_{б} = 2πRH $

Рассматривая половину треугольника в основании цилиндра, находим

$ sin(\frac{α}{2}) = \frac{\frac{a}{2}}{R} $

Откуда находим радиус цилиндра

$ R = \frac{\frac{a}{2}}{sin(\frac{α}{2})} $

и

$ |O_{1}M| = Rcos(\frac{α}{2})=\frac{acos(\frac{α}{2})}{2sin(\frac{α}{2})}=\frac{a}{2tg(\frac{α}{2})} $

Рассматривая треугольник O1O2M

$ tg(φ) = \frac{H}{O_{1}M} $

Откуда находим высоту цилиндра

$ H = (O_{1}M)tg(φ)=\frac{atg(φ)}{2tg(\frac{α}{2})} $

Подставляем найденные значения радиуса и высоты

$ S_{б} = 2π\frac{\frac{a}{2}}{sin(\frac{α}{2})}\frac{atg(φ)}{2tg(\frac{α}{2})}=\frac{πa^{2}tg(φ)}{2sin(\frac{α}{2})tg(\frac{α}{2})} $

Комментарии

Оставить комментарий

Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь