Найти длину третьей стороны треугольника Тема задачи: Построение и исследование геометрических фигур
Тема задачи: Построение и исследование геометрических фигур
 Создано:
@kirill
29 октября 2015
13:04
Создано:
@kirill
29 октября 2015
13:04
Стороны треугольника номер один равны 17, 25 и 26. В треугольнике номер два известно две стороны 17 и 25. Найти длину третьей стороны, еслиу треугольников равны радиусы вписанных окружностей Решения задачи
Данные задачи: в два треугольника вписаны окружности
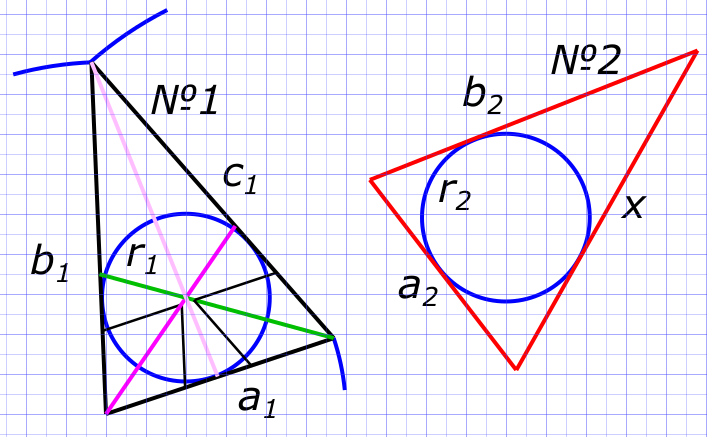
Изобразим на рисунке условия задачи Воспользуемся теоремой: $В любой треугольник можно вписать окружность и при том только одну$ Уравнение вписанной окружности
$ r = \frac{S}{p} $ Где:
$ r - радиус вписанной окружности; $
$ S - площадь треугольника $ и
$ p - полупериметр $ Находим
$ p_{1} = \frac{a_{1}+b_{1}+c_{1}}{2}=\frac{17+25+26}{2}=34 $ Так как r1=r2, то
$ p_{2} = \frac{a_{2}+b_{2}+c_{2}}{2}=\frac{17+25+x}{2}=34 $ Откуда находим
$ x = 2 × 34 -17 - 25 = 26 $ Ответ:
$ Длина третьей стороны c_{2} = 26 $ КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все геометры |
Комментарии