Указать расстояние между точками C и D, если AD= 2 корень из 3 см

Угол между плоскостями равностонних треугольников ABC и ABD равен 60 градусам. Указать расстояние между точками C и D, если AD= 2 корень из 3 см

Оцените сложность задачи:

1 голосов, средняя сложность: 5.0000

Решения задачи

поставьте оценку:

0 голосов, средний бал: 0.0000

Данные задачи: равностронние треугольники ABC и ABD

Угол между плоскостями равносторонних треугольников

град

Расстояние между точками AD

$2\sqrt{3}$

Определить расстояние между точками CD

|CD|

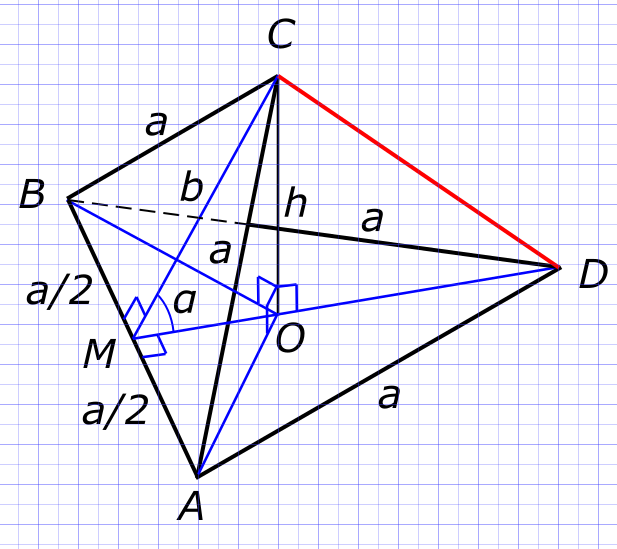
Изобразим на рисунке условия задачи

В прямоугольном треугольнике AMC

$ (BC)^{2} = (BM)^{2}+(CM)^{2} $

Откуда находим

$ CM = \sqrt{(BC)^{2}-(BM)^{2}}=\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=3 $

В прямоугольном треугольнике OMC

$ \frac{OM}{MC} = cos{α} $

$ \frac{OC}{MC} = sin(α) $

Откуда находим

$ OM = (MC)cos(α)=3×\frac{1}{2}=\frac{3}{2} $

$ OC = (MC)sin(α)=3×\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2} $

В прямоугольном треугольнике AMD

$ (AD)^{2} = (MD)^{2}+(AM)^{2} $

Откуда находим

$ (MD) = \sqrt{(AD)^{2}-(AM)^{2}}=\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=3 $

$ OD = MD-OM = 3- \frac{3}{2}=\frac{3}{2} $

В прямоугольном треугольнике OCD

$ CD = \sqrt{(OC)^{2}+(OD)^{2}}=\sqrt{(\frac{3\sqrt{3}}{2})^{2}+(\frac{3}{2})^{2}}=3 $

Ответ:

$ расстояние между точками CD равно 3 $