Даны вершины треугольника АВС. Найти: 1)Длину стороны АВ. 2) внутренний угол А в радианах с точностью до двух знаков после запят Тема задачи: Нахождение площадей фигур
Тема задачи: Нахождение площадей фигур
 Создано:
@1q2w3e
17 декабря 2016
20:57
Создано:
@1q2w3e
17 декабря 2016
20:57
A(-5;7), B(7;-2), C(11;20) Даны вершины треугольника АВС. Найти: 1)Длину стороны АВ. 2) внутренний угол А в радианах с точностью до двух знаков после запятой. 3) уравнение медианы СМ. 4) уравнение высоты СК. 5) точку пересечения высот (т. F). 6) площадь треугольника АВС. Сделать чертеж. Решения задачи
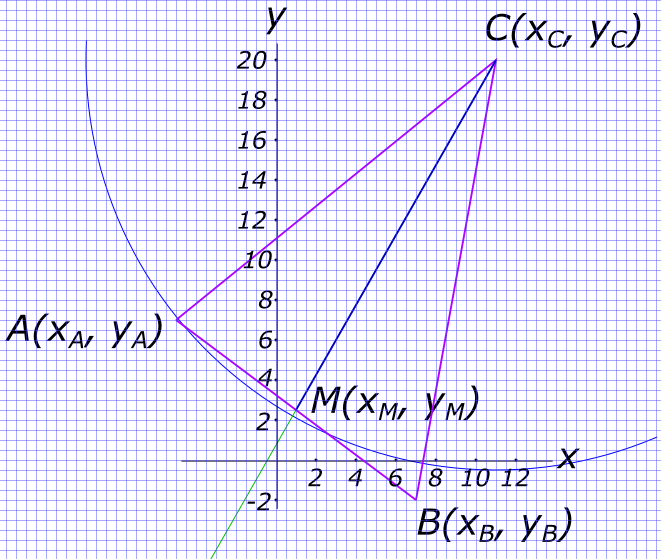
Изобразим на рисунке условия задачи Длина стороны треугольника находится по формуле
$ |AB| = \sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}} $ подставляем в формулу значения координат
$ |AB| = \sqrt{(7+5)^{2}+(-2-7)^{2}}=\sqrt{(12)^{2}+(-9)^{2}}=15 $ Чтобы найти угол A, необходимо узнать длину стороны AC
$ |AC| = \sqrt{(11+5)^{2}+(20-7)^{2}}=\sqrt{(16)^{2}+(13)^{2}}=20,61 $ формула 4
$ \vect{AB} = (7+5; -2-7)=(12; -9) $ формула 5
$ \vect{AC} = (11+5; 20-7)=(16; 13) $ формула 6
$cos(⦟A)=cos(\vect{AB}^\vect{AC})=\frac{\vect{AB}×\vect{AC}}{|AB|×|AC|}=\frac{12×16+(-9)×13}{15×20,61}=0,24$ формула 7
$ ⦟A = arccos(⦟A)=arccos(0.24)=1,33 рад $ Переводим радианы в градусы
$ ⦟A = \frac{0,90×180}{3,14}=76.24° $ Находим координаты точки M
$ x_{M} = \frac{x_{A}+x_{B}}{2}=\frac{-5+7}{2}=1 $ и
$ y_{M} = \frac{7+(-2)}{2}=2,5 $
$ M(1; 2,5) $ Уравнение прямой через две точки (медианы CM)
$ CM = \frac{x-x_{C}}{x_{M}-x_{C}}=\frac{y-y_{C}}{y_{M}-y_{C}} $ подставив значения координат, получаем
$ \frac{x-11}}{1-11}=\frac{y-20}}{\frac{5}{2}-20} $ Откуда находим
$ y=(x-11)(5-40)=-20(y-20) $ Раскрываем скобки
$ -35x+385=-20y+400 $ Откуда находим
$ 20y-35x-15=0 $ Делим левую и правую части уравнения на 5
$ 4y-7x-3=0 $ Ответ:
$ Длина стороны AB равна 15; $
$ Внутренний угол при вершине A равен 76,24°; $
$ Уравнение медианы CM: y=\frac{7}{4}x+\frac{3}{4}. $ КомментарииДаны вершины треугольника АВС. Найти: а) Длину стороны АВ. b) внутренний угол А в радианах с точностью до двух знаков после запятой. c) уравнение медианы СМ. d) уравнение высоты СК. e) точку пересечения высот (т. F). f) площадь треугольника АВС. Сделать чертеж. КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все геометры |
Комментарии