Все решения геометра Ичиго Банкайнайти sin tan ctan.
Пример текста формула 1
$ \sin^{2}(\alpha)+\cos^{2}(\alpha) = 1 $ формула 2
$ \sin(\alpha) = \sqrt{1 - \cos^{2}(\alpha)} $ формула 3
$ \sin(\alpha) = \sqrt{1 - \frac{3}{4}} = \sqrt{\frac{1}{4}} = \frac{1}{2} $ формула 4
$ \tg(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} $ формула 5
$ \tg(\alpha) = \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}} $ формула 6
$ \ctg(\alpha) = \frac{\cos(\alpha)}{\sin(\alpha)} $ формула 7
$ \ctg(\alpha) = \frac{\sqrt{3}/2}{1/2} = \sqrt{3} $ Найти площадь трапеции
Спустим перпендикуляр на AB из точки D. 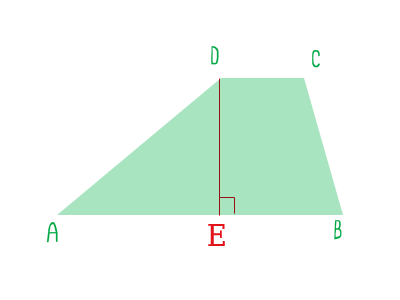
рисунок 1 В треугольнике AED нам известно: формула 1
$ угол A = 30 градусов $ формула 2
$ угол E = 90 градусов $ формула 3
$ угол D = 180 - (30 + 90) = 60 градусов $ формула 4
$ гипотенуза AD = 16 $ Из прямоугольного треугольника найдем высоту DE формула 5
$ DE = AD * \sin(A) = 16 * \sin(30) = 16 * 0.5 = 8 $ Спустим еще один перпендикуляр на AB из точки С. 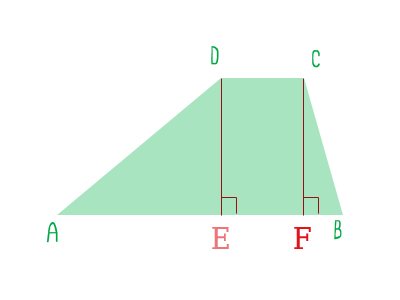
рисунок 2 Вся фигура разбита на три фигуры: Треугольник AED, прямоугольник DEFC, и треугольник BCF. Сумма их площадей и равна искомой площади. Площадь треугольника AED формула 6
$ S_{AED} = \frac{1}{2} AE * DE $ Площадь прямоугольника DEFC формула 7
$ S_{DEFC} = DC * DE $ Площадь треугольника BCF формула 8
$ S_{BCF} = \frac{1}{2} BF * CF $ В треугольнике AED не хватает стороны AE формула 9
$ AE = AD * \sin(D) = 16 * \sin(60) = 16 * \frac{\sqrt{3}}{2} = 8 * \sqrt{3} $ формула 10
$ S_{AED} = \frac{1}{2} * 8 * \sqrt{3} * 8 = 32 * \sqrt{3} $ формула 11
$ S_{DEFC} = 4 * 8 = 32 $ В треугольнике BCF формула 12
$ FB = AB - (AE+EF) = 32 - (8 * \sqrt{3} + 4) $ формула 13
$ FB = 4*(8-2*\sqrt{3}-1) $ формула 14
$ S_{BCF} = \frac{1}{2} * 4 * (7-2 * \sqrt{3}) * 8 $ формула 15
$ S = 32 * \sqrt{3} + 32 + \frac{1}{2} * 32 * (7-2 * \sqrt{3}) $ формула 16
$ S = 32 * ( \sqrt{3} + 1 + \frac{7}{2} - \sqrt{3}) $ формула 17
$ S = 32 + 7*16 = 144 $ Ответ 144 Комментарии |
Записать новую задачу Все задачи Все темы Все геометры |


Комментарии