Все решения геометра @NICKНайдите площадь сечения пирамиды плоскостью
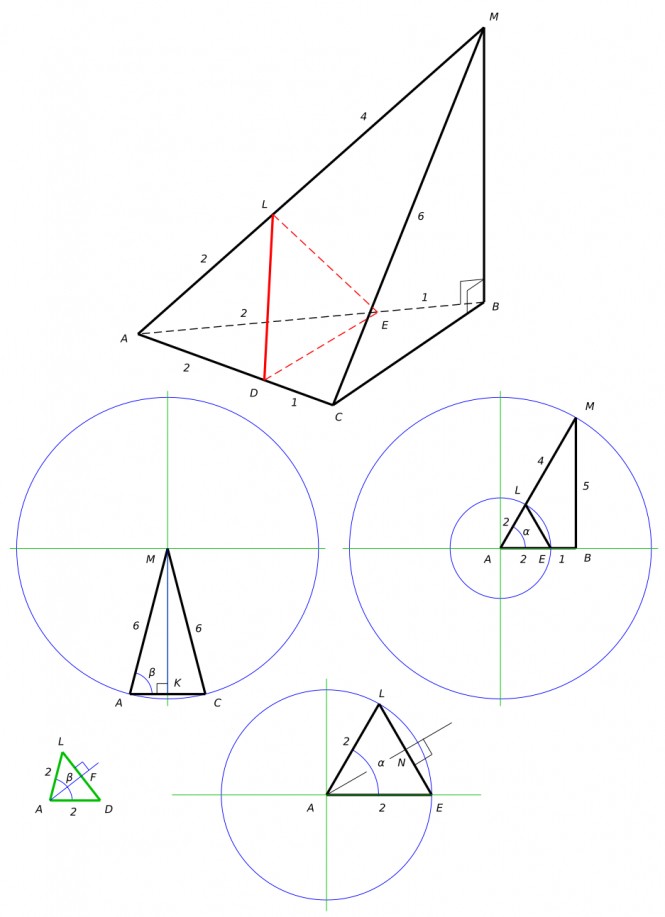
В треугольной пирамиде MABC основанием является правильный треугольник ABC, ребро MB перпендикулярно плоскости основания, стороны основания равны 3, а ребро MA равно 6. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM точка L. Известно, что AD=AL=2, и BE=1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E,D и L. Изобразим условие задачи на рисунке Рассматривая треугольники ABC и ADE находим
$ ∆ABC ∾ ∆ADE ⇒ DE=AD=2 $ Рассматривая прямоугольный треугольник AMB находим с помощью теоремы Пифагора
$ MB=\sqrt{AM^{2}-AB^{2}}=MB=\sqrt{6^{2}-3^{2}}=5 $ Рассматривая треугольник AMB находим
$ sinα = \frac{MB}{AM}=\frac{5}{6} $ Рассматривая треугольник ALE находим
$ sin(\frac{α}{2})=\frac{NE}{AE}=\frac{\frac{1}{2}LE}{AE} $ Откуда
$ LE = 2AEsin(\frac{α}{2}) $
$ α = arcsinα=0,9851 рад $ Тогда
$ sin(\frac{α}{2}) = 0,472858 $ И
$ LE = 2AEsin(\frac{α}{2})=2×2×0,472858=1,8914 $ Рассматривая треугольник AMC находим
$ cosβ = \frac{AK}{AM}=\frac{\frac{AC}{2}}{AM}=\frac{\frac{3}{2}}{6}=\frac{1}{4} $ Откуда
$ β = arccosβ = 0,9689 рад $ Рассматривая треугольник ADL находим
$ sin(\frac{β}{2}) = \frac{LF}{AL}=\frac{\frac{DL}{2}}{AL} $ Откуда
$ DL = 2ALsin(\frac{β}{2}) = 2×2sin(0,48445621)=1,8629 $ Таким образом найдены все стороны треугольника сечения. Его площадь находим по формуле Герона
$ S = \sqrt{p(p-a)(p-b)(p-c)} $ Где
$ p = \frac{a+b+c}{2}=\frac{2+1,8914+1,8629}{2}=2,877 $ Тогда
$ S_{∆EDL} = \sqrt{2,877(0,877)(0,986)(1,014)}=1,588 $ Ответ: площадь сечения пирамиды плоскостью, проходящей через точки E,D и L
$ S_{∆EDL} = 1,588 $ Найти периметр.
Найти периметр 
Найти периметр формула 1
$ P_{AMK} = AM+MK+KA $ формула 2
$ AM = \frac{1}{2}AB = \frac{1}{2}6 = 3 $ формула 3
$ AK = \frac{1}{2}AD $ Из пропорциональности сторон треугольников следует
$ ABD ∾ AMK $ формула 5
$ sin(30°) = \frac{AM}{MK} = \frac{1}{2} $ Откуда
$ MK = 2AM $ И оконччательно
$ P_{AMK} = \frac{1}{2}AB + 2AM + \frac{1}{2}AD = 3 + 2×3 + 7,5 = 16,5 $ КомментарииНайти среднюю линию трапеции
Найти среднюю линию трапеции 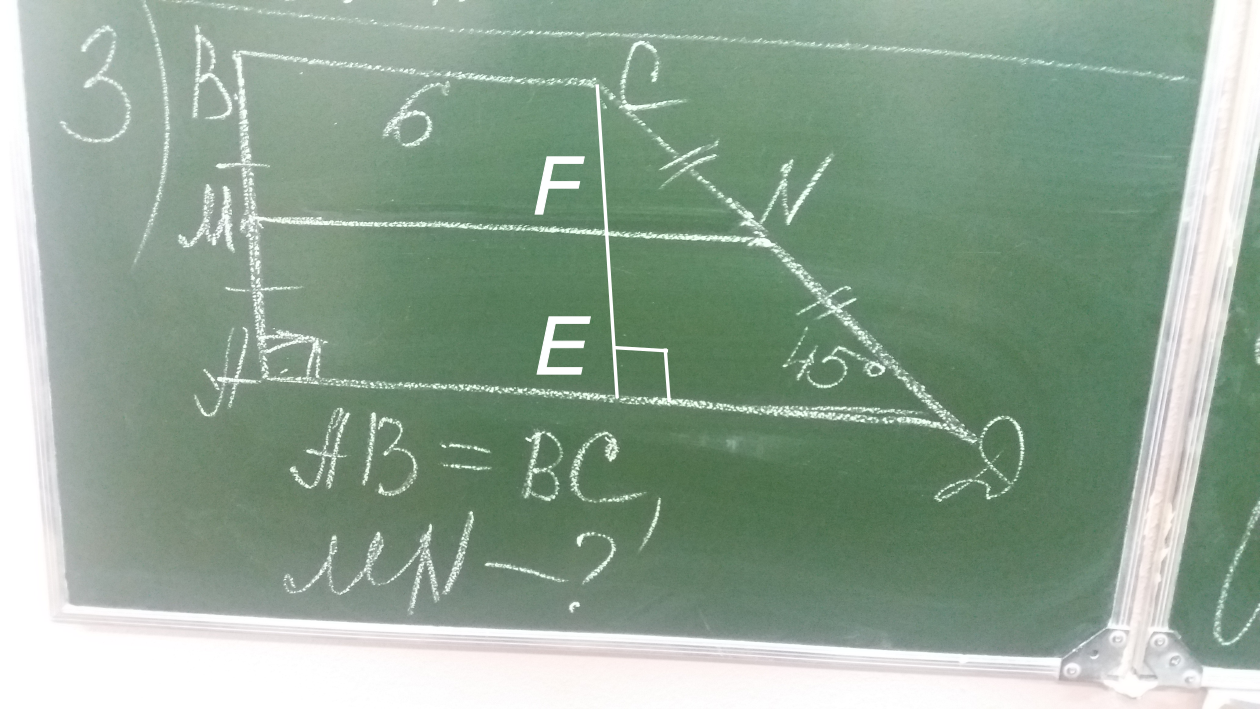
Найти среднюю линию трапеции формула 1
$ AB = CE; BC = MF $ формула 2
$ CF = FE = BM = \frac{1}{2}AB $ формула 3
$ FN = CF = \frac{1}{2}AB $ формула 4
$ MN = MF + FN = BC + \frac{1}{2}AB = BC + \frac{1}{2}BC = 6 + \frac{1}{2}6 = 9 $ КомментарииОпечатка наверное. 6+3=9
Найти диагональ параллелограмма
Данные задачи: параллелограмм ABCD
Периметр параллелограмма ABCD
$ P = 2 AB +2 BC $ Но
$ AB - BC = 3 $ Откуда
$ AB = 3 + BC $ Тогда
$ P = 2 (3 + BC) + 2BC = 50 $ Откуда
$ BC = \frac{50-6}{4} = \frac{27}{2} $ и
$ AB = 3 + BC = 3 + \frac{27}{2} = \frac{33}{2} $ Из треугольника ABD по теореме Пифагора находим
$ BD = \sqrt{(AB)^{2}-(BC)^{2}} = 3\sqrt{10} $ КомментарииНайти длину гипотенузы
Через середину гипотенузы прямоугольного треугольника проведен перпендикуляр ...
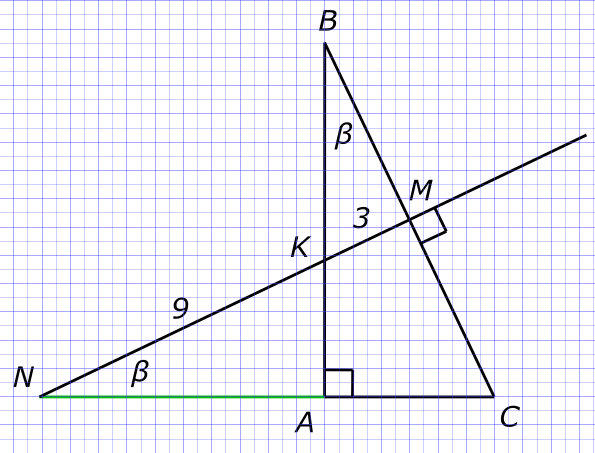
Изобразим на рисунке условия задачи Прямоугольные треугольники ABC, KBM и MNC подобны так как
$ ⦟C ∈ ∆ABC и ∆NMC $ и углы образованные взаимно перпендикулярными сторонами
$ ⦟MNC = ⦟ABC = β $ как углы образованные взаимно перпендикулярными сторонами
$ ⦟BKM = ⦟BCA $ Из треугольника KBM
$ tg(β) = \frac{KM}{BM} $ Из треугольника NMC
$ tg(β) = \frac{MC}{MN} $ Приравниваем правые части уравнений
$ \frac{KM}{BM} = \frac{MC}{MN} $ Откуда находим
$ BM = \sqrt{(KM)(MN)}=\sqrt{(3)(3+9)}=6 $ И окончательно
$ BC = 2(BM) = 2 × 6 = 12 $ Ответ:
$ Длина гипотенузы равна 12 $ КомментарииНайти площадь треугольника
Данные задачи: треугольник ABC на расходящихся прямых
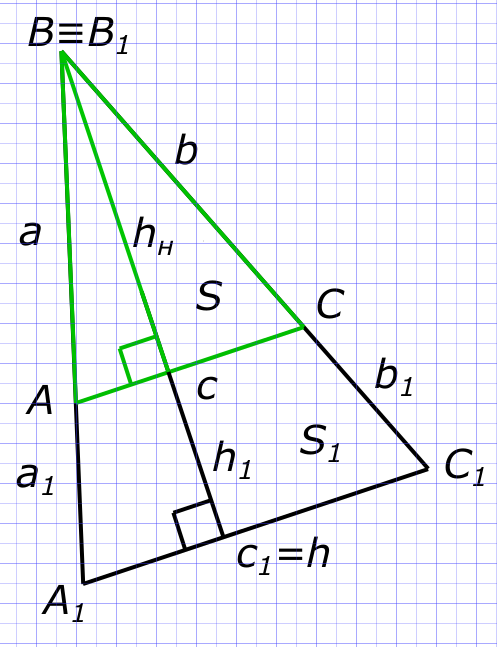
Изобразим на рисунке условия задачи Треугольники ABC и A1B1C1 подобны так как
$ ⦟A = A_{1}; ⦟B = ⦟ B_{1}; ⦟C = ⦟C_{1} $ и
$ \frac{AB}{A_{1}B_{1}} = \frac{BC}{B_{1}C_{1}} = \frac{CA}{C_{1}A_{1}} = k $ Площадь треугольника начальная
$ S = \frac{1}{2}ch_{н} $ Площадь треугольника увеличенная
$ S_{1} = \frac{1}{2}c_{1}h_{1} $ Разделим первое уравнение на второе
$ \frac{S}{S_{1}} = \frac{c}{c_{1}} × \frac{h_{н}}{h_{1}} = k × k = k^{2} $ Откуда находим
$ S_{1} = \frac{S}{k^{2}} $ Ответ:
$ Площадь треугольника увеличенная равна \frac{S}{k^{2}} $ КомментарииНайти длину третьей стороны треугольника
Данные задачи: в два треугольника вписаны окружности
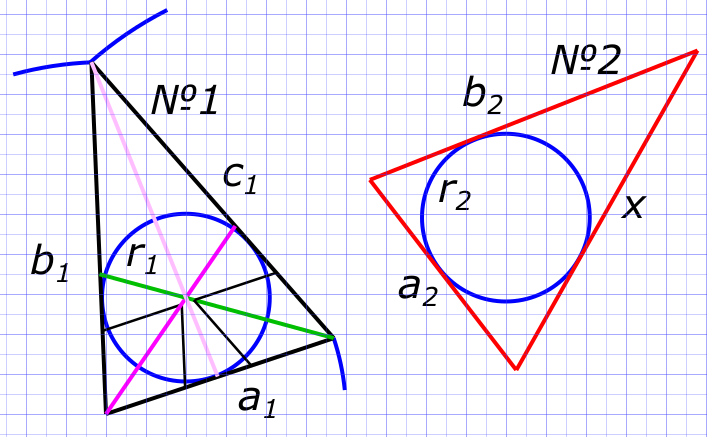
Изобразим на рисунке условия задачи Воспользуемся теоремой: $В любой треугольник можно вписать окружность и при том только одну$ Уравнение вписанной окружности
$ r = \frac{S}{p} $ Где:
$ r - радиус вписанной окружности; $
$ S - площадь треугольника $ и
$ p - полупериметр $ Находим
$ p_{1} = \frac{a_{1}+b_{1}+c_{1}}{2}=\frac{17+25+26}{2}=34 $ Так как r1=r2, то
$ p_{2} = \frac{a_{2}+b_{2}+c_{2}}{2}=\frac{17+25+x}{2}=34 $ Откуда находим
$ x = 2 × 34 -17 - 25 = 26 $ Ответ:
$ Длина третьей стороны c_{2} = 26 $ КомментарииНайти радиусы окружностей и длину хорды AD
Данные задачи: две окружности внутренне касаются друг друга в точке А
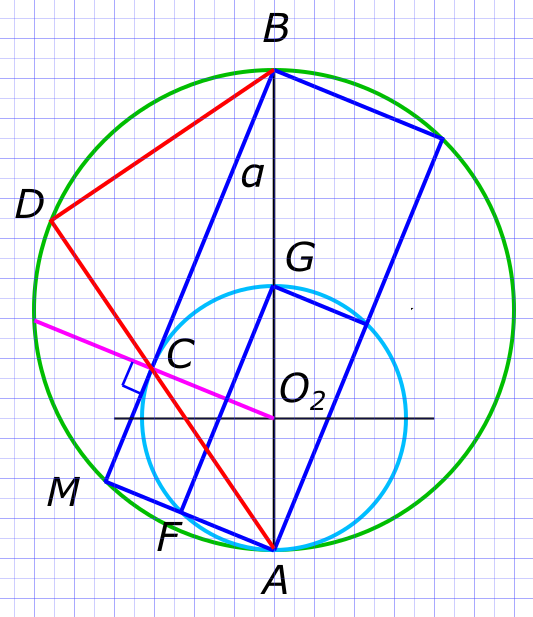
Изобразим на рисунке условия задачи Диаметры большой и малой окружностей - AB и AG, тогда
$ ⦟AMB = ⦟AFG = 90° $ Так как опирается на полуокружность По двум углам
$ ∆AMB ∾ ∆AFG $ Тогда
$ \frac{MB}{GF} = \frac{AB}{GA} = \frac{AM}{AF} $ Так как
$ GF = 2 MC = 2 × 2,4 = 4,8 $ Тогда
$ \frac{2,4+4}{4,8} = \frac{2r_{1}}{2r_{2}} $ Откуда находим
$ r_{1} = \frac{6,4}{4,8}r_{2} = 1,33 r_{2} $ Из прямоугольного треугольника BCO2 по теореме Пифагора
$ (BO_{2})^{2}=(CO_{2})^{2}+(CB)^{2} $ Подставив значения
$ (2 r_{1}-r_{2})^{2}=(r_{2})^{2}+(4)^{2} $ или
$ (2 × 1,33 r_{2}-r_{2})^{2}=(r_{2})^{2}+16 $ формула 10
$ (1,66 r_{2})^{2}=(r_{2})^{2}+16 $ Откуда находим
$ r_{2} = \sqrt{\frac{16}{0,66}}=4,92 $ и
$ r_{1} = 1,33 r_{2} = 1,33 × 4,92 = 6,54 $ Воспользуемся теоремой о произведении отрезков пересекающихся хорд
$ BM ∩ AD = C $ и
$ BC × CM = AC × CD $ Из прямоугольного треугольника AMB находим
$ AM = \sqrt{(AB)^{2}-(BM)^{2}}=\sqrt{(13,08)^{2}-(6,4)^{2}}=11,41 $ Из прямоугольного треугольника AMC находим
$ AC = \sqrt{(CM)^{2}+(AM)^{2}}=\sqrt{(2,4)^{2}+(11,41)^{2}}=11,66 $ Подставляем значения в уравнение
$ 4 × 2,4 = 11,66 × CD $ Откуда находим
$ CD = \frac{4 × 2,4}{11,66}=0,82 $ и
$ AD = AC+CD = 11,66 + 0,82 = 12,48 $ Ответ:
$ Радиусы большой и малой окружности 6,54 и 4,92 $
$ Длина хорды AD равна 12,48 $ КомментарииУказать расстояние между точками C и D, если AD= 2 корень из 3 см
Данные задачи: равностронние треугольники ABC и ABD
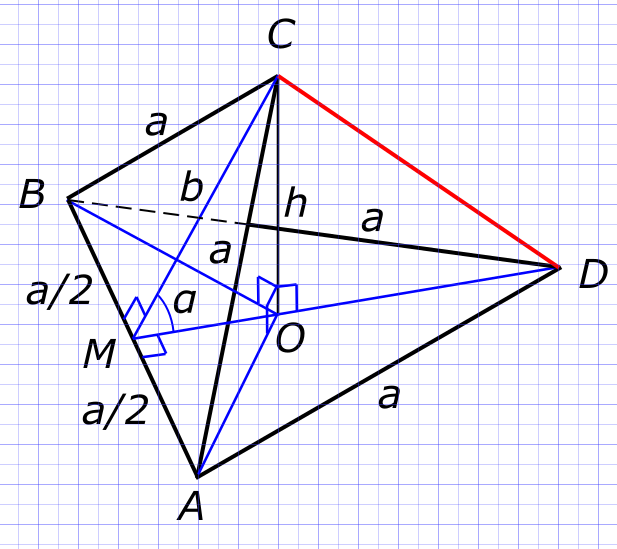
Изобразим на рисунке условия задачи В прямоугольном треугольнике AMC
$ (BC)^{2} = (BM)^{2}+(CM)^{2} $ Откуда находим
$ CM = \sqrt{(BC)^{2}-(BM)^{2}}=\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=3 $ В прямоугольном треугольнике OMC
$ \frac{OM}{MC} = cos{α} $ и
$ \frac{OC}{MC} = sin(α) $ Откуда находим
$ OM = (MC)cos(α)=3×\frac{1}{2}=\frac{3}{2} $ и
$ OC = (MC)sin(α)=3×\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2} $ В прямоугольном треугольнике AMD
$ (AD)^{2} = (MD)^{2}+(AM)^{2} $ Откуда находим
$ (MD) = \sqrt{(AD)^{2}-(AM)^{2}}=\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=3 $ и
$ OD = MD-OM = 3- \frac{3}{2}=\frac{3}{2} $ В прямоугольном треугольнике OCD
$ CD = \sqrt{(OC)^{2}+(OD)^{2}}=\sqrt{(\frac{3\sqrt{3}}{2})^{2}+(\frac{3}{2})^{2}}=3 $ Ответ:
$ расстояние между точками CD равно 3 $ КомментарииНайти S основания и S боковой поверхности и объём правильной n-угольной пирамиды
Данные задачи: правильная трехгранная пирамида
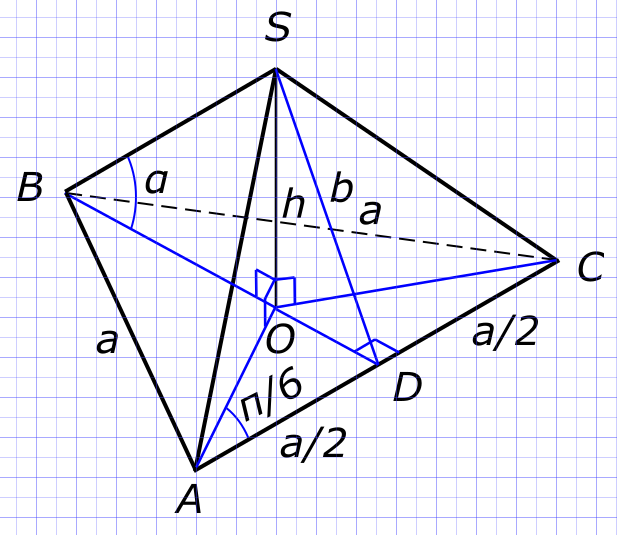
Изобразим графически условие задачи В прямоугольном треугольнике OSB:
$ sin(α) = \frac{OS}{BS} = \frac{h}{BS} $ Откуда находим длину бокового ребра пирамиды
$ BS = \frac{h}{sin(α)} $ и
$ cos(α) = \frac{OB}{BS} = \frac{OB}{\frac{h}{sin(α)}} $ Откуда находим
$ OB = OA = OC = \frac{h}{tg(α)} $ В прямоугольном треугольнике AOD:
$ \frac{OD}{OA} = sin(\frac{π}{6}) = \frac{1}{2} $ Откуда находим
$ OD = OA\frac{1}{2} = \frac{1}{2}\frac{h}{tg(α)} $ и
$ \frac{\frac{a}{2}}{OA} = cos(\frac{π}{6}) = $ Откуда находим
$ a = OA cos(\frac{π}{6}) = \frac{\sqrt{3}h}{tg(α)} $ Находим площадь основания пирамиды
$ S_{осн} = \frac{1}{2}a(OB+OD)=\frac{1}{2}\frac{\sqrt{3}h}{tg(α)}(\frac{3}{2}\frac{h}{tg(α)})=\frac{3\sqrt{3}h^{2}}{4(tg(α))^{2}} $ Находим площадь боковой поверхности
$ S_{б} = 3\frac{1}{2}a(SD)=3\frac{1}{2}a\sqrt{h^{2}+(OD)^{2}}=\frac{3}{2}\frac{\sqrt{3}h}{tg(α)}\sqrt{h^{2}+( \frac{1}{2}\frac{h}{tg(α)})^{2}} $ Находим объем пирамиды
$ V = \frac{hna}{12tg(\frac{180}{n})}=a\frac{hn}{12\sqrt{3}}=\frac{\sqrt{3}h}{tg(α)}\frac{hn}{12\sqrt{3}}=\frac{nh^{2}}{12tg(α)} $ КомментарииНайти расстояние от точки А до плоскости α
Пример текста Данные задачи: Из точки А к плоскости α проведены две наклонные
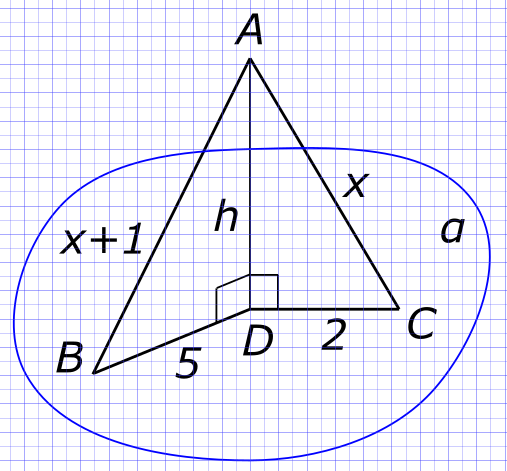
Изобразим на рисунке условия задачи Из прямоугольного треугольника ACD
$ (AD)^{2} = (AC)^{2}-(CD)^{2}=x^{2}-2^{2} $ Из прямоугольного треугольника ABD
$ (AD)^{2} = (AВ)^{2}-(BD)^{2}=(x+1)^{2}-5^{2} $ Тогда
$ x^{2}-2^{2} = (x+1)^{2}-5^{2} $ или
$ x^{2}-4 = x^{2}+2x+1-25 $ Откуда находим
$ x = \frac{20}{2}=10 $ Тогда
$ AC = x = 10 см $ и
$ AB = x+1 = 10+1 = 11 см $ Находим расстояние, например из треугольника ABD
$ h = AD = \sqrt{(AB)^{2}-(BD)^{2}}=\sqrt{11^{2}-5^{2}}=\sqrt{96} см $ Ответ:
$ Расстояние от точки А до плоскости α равно \sqrt{96} см $ КомментарииНайти площадь равнобедренного треугольника
Данные задачи: равнобедренный треугольник
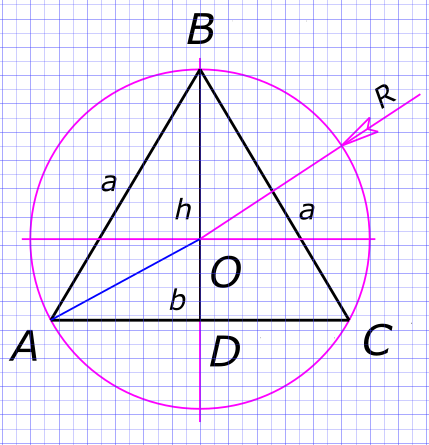
Изобразим на рисунке условия задачи Треугольник равнобедренный, поэтому центр описанной окружности
$ O ∈ BD $
$ OA = OB = R = 17 $
$ OD = BD - OA = 25 - 17 = 8 $ По теореме Пифагора
$ AD = \sqrt{(OA)^{2}-(OD)^{2}}=\sqrt{17^{2}-8^{2}}=15 $
$ b = AC = 2AD = 2 × 15 = 30 $ Тогда
$ S = \frac{1}{2}bh = \frac{1}{2}30×25 = 375 $ Ответ:
$ Площадь треугольника равна 375 $ КомментарииНайти периметр параллелограмма
Данные задачи:
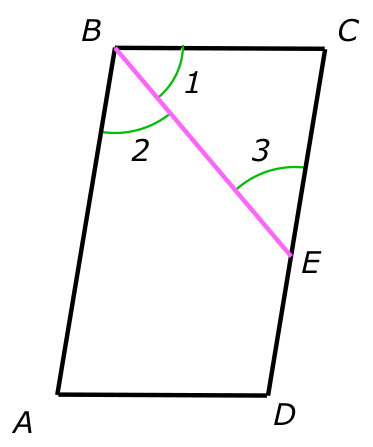
Изобразим на рисунке условия задачи Так как, BE - биссектриса угла при вершине B, то
$ ⦟1 = ⦟2 $ Углы 2 и 3 накрест лежащие при параллельных прямых AB и CD и секущей BE, следовательно
$ ⦟2 = ⦟3 $ По признаку равенства углов при основании BE
$ ∆BCE - равнобедренный $ Следовательно
$ BC = CE = 3 см $ Периметр параллелограмма
$ P_{ABCD} = 2(BC+(CE+ED))=2(3+(3+2))=16 см $ Ответ:
$ Периметр параллелограмма равен 16 см $ КомментарииДаны вершины треугольника АВС. Найти: 1)Длину стороны АВ. 2) внутренний угол А в радианах с точностью до двух знаков после запят
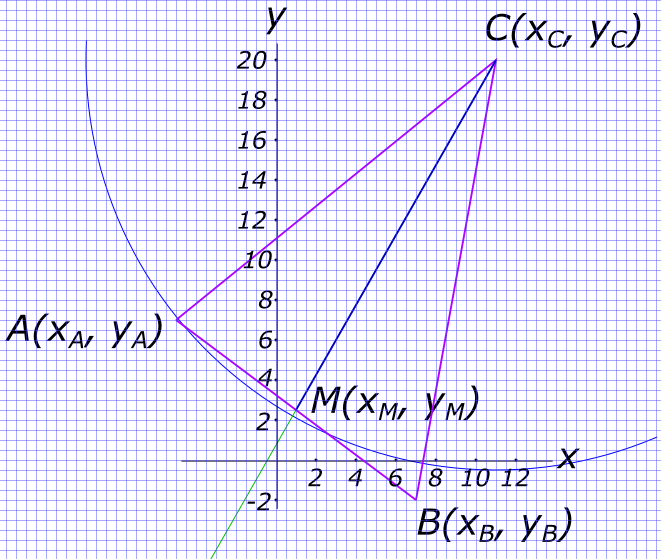
Изобразим на рисунке условия задачи Длина стороны треугольника находится по формуле
$ |AB| = \sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}} $ подставляем в формулу значения координат
$ |AB| = \sqrt{(7+5)^{2}+(-2-7)^{2}}=\sqrt{(12)^{2}+(-9)^{2}}=15 $ Чтобы найти угол A, необходимо узнать длину стороны AC
$ |AC| = \sqrt{(11+5)^{2}+(20-7)^{2}}=\sqrt{(16)^{2}+(13)^{2}}=20,61 $ формула 4
$ \vect{AB} = (7+5; -2-7)=(12; -9) $ формула 5
$ \vect{AC} = (11+5; 20-7)=(16; 13) $ формула 6
$cos(⦟A)=cos(\vect{AB}^\vect{AC})=\frac{\vect{AB}×\vect{AC}}{|AB|×|AC|}=\frac{12×16+(-9)×13}{15×20,61}=0,24$ формула 7
$ ⦟A = arccos(⦟A)=arccos(0.24)=1,33 рад $ Переводим радианы в градусы
$ ⦟A = \frac{0,90×180}{3,14}=76.24° $ Находим координаты точки M
$ x_{M} = \frac{x_{A}+x_{B}}{2}=\frac{-5+7}{2}=1 $ и
$ y_{M} = \frac{7+(-2)}{2}=2,5 $
$ M(1; 2,5) $ Уравнение прямой через две точки (медианы CM)
$ CM = \frac{x-x_{C}}{x_{M}-x_{C}}=\frac{y-y_{C}}{y_{M}-y_{C}} $ подставив значения координат, получаем
$ \frac{x-11}}{1-11}=\frac{y-20}}{\frac{5}{2}-20} $ Откуда находим
$ y=(x-11)(5-40)=-20(y-20) $ Раскрываем скобки
$ -35x+385=-20y+400 $ Откуда находим
$ 20y-35x-15=0 $ Делим левую и правую части уравнения на 5
$ 4y-7x-3=0 $ Ответ:
$ Длина стороны AB равна 15; $
$ Внутренний угол при вершине A равен 76,24°; $
$ Уравнение медианы CM: y=\frac{7}{4}x+\frac{3}{4}. $ КомментарииОпределить боковую поверхность цилиндра
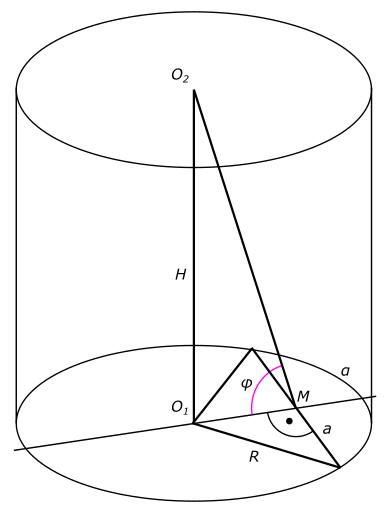
Изобразим на рисунке условия задачи Составим уравнение боковой поверхности цилиндра
$ S_{б} = 2πRH $ Рассматривая половину треугольника в основании цилиндра, находим
$ sin(\frac{α}{2}) = \frac{\frac{a}{2}}{R} $ Откуда находим радиус цилиндра
$ R = \frac{\frac{a}{2}}{sin(\frac{α}{2})} $ и
$ |O_{1}M| = Rcos(\frac{α}{2})=\frac{acos(\frac{α}{2})}{2sin(\frac{α}{2})}=\frac{a}{2tg(\frac{α}{2})} $ Рассматривая треугольник O1O2M
$ tg(φ) = \frac{H}{O_{1}M} $ Откуда находим высоту цилиндра
$ H = (O_{1}M)tg(φ)=\frac{atg(φ)}{2tg(\frac{α}{2})} $ Подставляем найденные значения радиуса и высоты
$ S_{б} = 2π\frac{\frac{a}{2}}{sin(\frac{α}{2})}\frac{atg(φ)}{2tg(\frac{α}{2})}=\frac{πa^{2}tg(φ)}{2sin(\frac{α}{2})tg(\frac{α}{2})} $ КомментарииНайдите синус, косинус и тангенс углов А и В треуголника АВС с прямым углом С
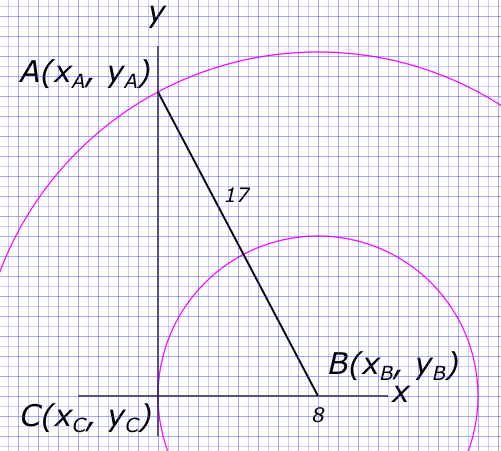
Изобразим на рисунке условия задачи a) Составляем уравнение длины гипотенузы прямоугольного треугольника
$ |AB| = \sqrt{(AC)^{2}+(BC)^{2}} $ Откуда находим
$ |AC|=\sqrt{(AB)^{2}-(BC)^{2}}=\sqrt{17^{2}-8^{2}}=15 $ Тогда:
$ sin(A) = \frac{AC}{AB}=\frac{15}{17}; $
$ cos(A) = \frac{BC}{AB}=\frac{8}{17} $ и
$ tg(A) = \frac{sin(A)}{cos(A)}=\frac{\frac{15}{17}}{\frac{8}{17}}=\frac{15}{8} $ КомментарииНаписать уравнение медианы mА, проведенной из вершины А.
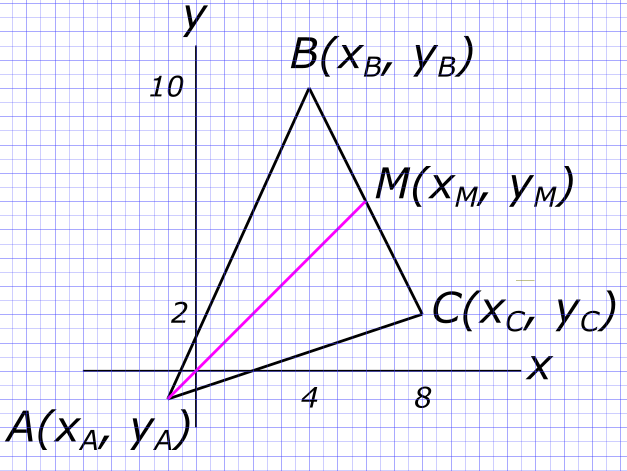
Изобразим на рисунке условия задачи Находим координаты точки M
$ M_{x} = \frac{x_{B}+x_{C}}{2}=\frac{4+8}{2}=6 $ и
$ M_{y} = \frac{y_{B}+y_{C}}{2}=\frac{10+2}{2}=6 $ Координаты точки M
$ M(6, 6) $ Уравнение прямой по двум точкам
$ \frac{x-x_{A}}{x_{M}-x_{A}} = \frac{y-y_{A}}{y_{M}-y_{A}} $ Подставляем значения
$ \frac{x-(-1)}{6-(-1)} = \frac{y-(-1)}{6-(-1)} $ или
$ \frac{x+1}{6+1} = \frac{y+1}{6+1} $ Откуда находим
$ y={6+1}\frac{x+1}{6+1}-1=x $ Ответ:
$ уравнение медианы: y = x $ КомментарииВычисление объема фигуры по переменным данным
Ребро жесткости представляет собой прямоугольную пластину толщиной S, в которой вырезаны два треугольника, отсюда
$ V = S[LH-\frac{1}{2}(a^{2}+(L-b)(H-b_{1}))] $ Комментарии |
Записать новую задачу Все задачи Все темы Все геометры |


Комментарии